PCA在图像降维的应用

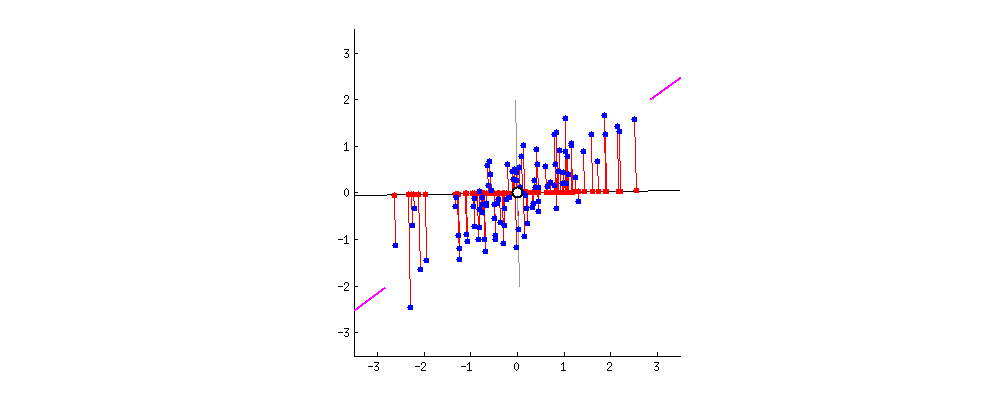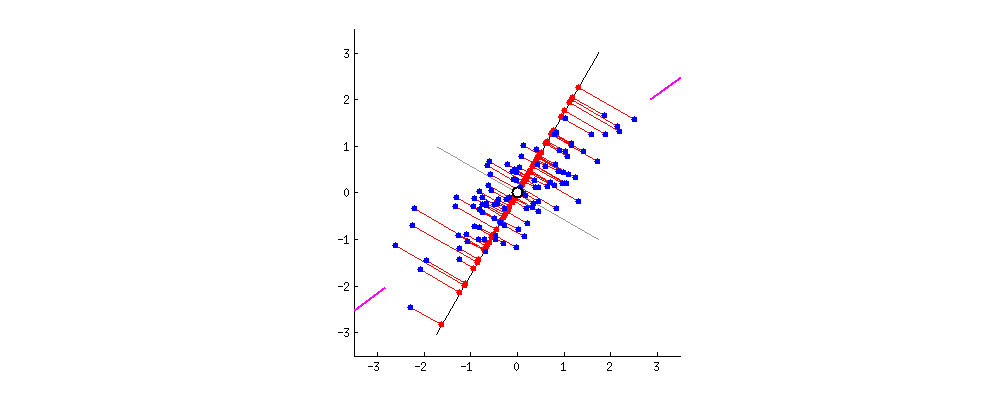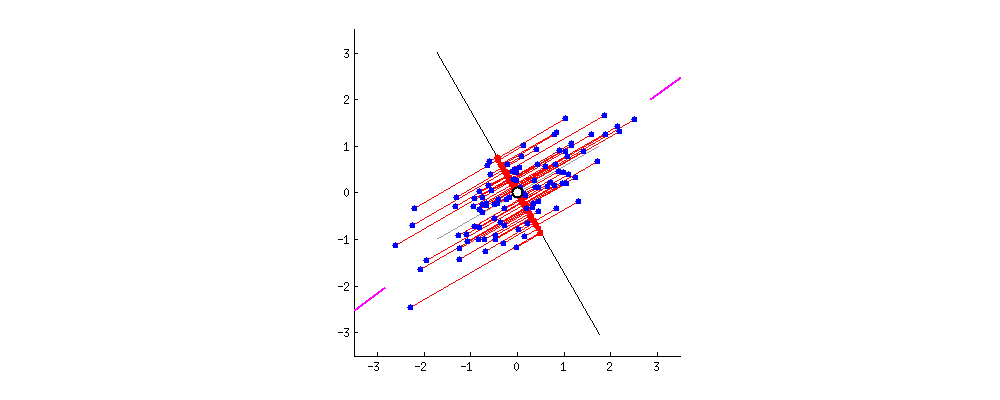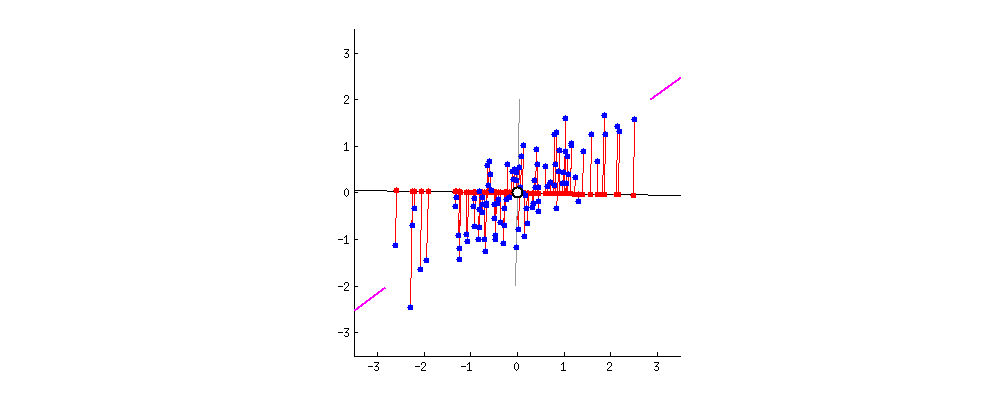
（自动编码器优化之主成分分析）从实例和数学背景的引导下详细的介绍了PCA的原理以及定义，并以旋转数据的角度论述其数据降维的实质，如何从降维之后的数据还原近似原始数据，以及如何选择主成分的个数。本篇文章将以简单的篇幅简单的介绍一下PCA在图像处理过程中的使用---降维。

为使PCA算法能有效工作，通常我们希望所有的特征 x[1], x[2], ... , x[n] 都有相似的取值范围（并且均值接近于0）。如果你曾在其它应用中使用过PCA算法，你可能知道有必要单独对每个特征做预处理，即通过估算每个特征 x[j] 的均值和方差，而后将其取值范围规整化为零均值和单位方差。但是，对于大部分图像类型，我们却不需要进行这样的预处理。假定我们将在自然图像上训练算法，此时特征 x[j] 代表的是像素 j 的值。所谓“自然图像”，不严格的说，是指人或动物在他们一生中所见的那种图像。

注：通常我们选取含草木等内容的户外场景图片，然后从中随机截取小图像块（如16x16像素）来训练算法。在实践中我们发现，大多数特征学习算法对训练图片的确切类型并不敏感，所以大多数用普通照相机拍摄的图片，只要不是特别的模糊或带有非常奇怪的人工痕迹，都可以使用。

在自然图像上进行训练时，对每一个像素单独估计均值和方差意义不大，因为（理论上）图像任一部分的统计性质都应该和其它部分相同，图像的这种特性被称作平稳性（stationarity）。

具体而言，为使PCA算法正常工作，我们通常需要满足以下要求：

(1)特征的均值大致为0；

(2)不同特征的方差值彼此相似。

对于自然图片，即使不进行方差归一化操作，条件(2)也自然满足，故而我们不再进行任何方差归一化操作（对音频数据,如声谱,或文本数据,如词袋向量，我们通常也不进行方差归一化）。实际上，PCA算法对输入数据具有缩放不变性，无论输入数据的值被如何放大（或缩小），返回的特征向量都不改变。更正式的说：如果将每个特征向量 x 都乘以某个正数（即所有特征量被放大或缩小相同的倍数），PCA的输出特征向量都将不会发生变化。

既然我们不做方差归一化，唯一还需进行的规整化操作就是均值规整化，其目的是保证所有特征的均值都在0附近。根据应用，在大多数情况下，我们并不关注所输入图像的整体明亮程度。比如在对象识别任务中，图像的整体明亮程度并不会影响图像中存在的是什么物体。更为正式地说，我们对图像块的平均亮度值不感兴趣，所以可以减去这个值来进行均值规整化。

具体的步骤是，如果 x[^i] 代表16x16的图像块的亮度（灰度）值（n=256 ），可用如下算法来对每幅图像进行零均值化操作：

请注意：

1）对每个输入图像块 x[^i] 都要单独执行上面两个步骤;

2）这里的 u[^i] 是指图像块 x[i] 的平均亮度值。尤其需要注意的是，这和为每个像素 x[j] 单独估算均值是两个完全不同的概念。

如果你处理的图像并非自然图像（比如，手写文字，或者白背景正中摆放单独物体），其他规整化操作就值得考虑了，而哪种做法最合适也取决于具体应用场合。但对自然图像而言，对每幅图像进行上述的零均值规整化，是默认而合理的处理。