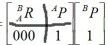球心坐标与本地坐标

1球心坐标(ECEF)与本地坐标(NEU)

假如你来到一个陌生城市，你很可能需要问路、通常会告诉你向北走100米，右转，向东走100米，理解起来很直观。你给儿子买了一个地球仪，你从北京(39,115)转到伦敦 (51,0)，这个动作就可以分解为两步：先转到同一个经度(39,0)，在转到同一个维度(51,0)

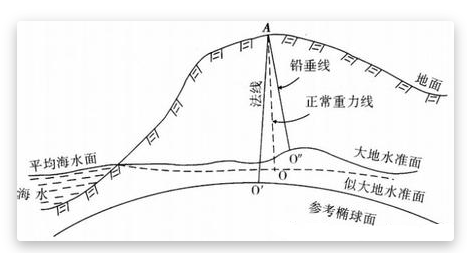
这个例子体现了一个问题：不同的地理范围下会使用更适合的坐标系。比如前者是局部的平面坐标，而后者是球面坐标。因此，同一个点相对不同的原点，具有不同的相对位置：既是地球上的一个经纬度，又是“出门右转富士康”的这类的位置。如图，蓝色坐标系就是球心坐标，而绿色坐标系是以球面一点为原点的本地坐标系。准确讲，就是该点对应球的切面和法线组成的空间。

这自然引出了这个问题：如何从以球心为原点的球面坐标到以球面上任意一点为原点的局部坐标，坐标系之间的转换，答案就是矩阵。

坐标系的换算，其实就是坐标原点之间的转换。比如发射导弹，首先瞄准，然后发射，这里面就包括两个动作：旋转和平移。如上图，旋转分为两步，经度（Z轴）旋转和纬度（X轴）旋转，分别是上图中绿色和蓝色两个过程。

如上，假设该经纬度对应的笛卡尔坐标为(XYZ),这就是从球心原点到该点的平移，两者结合得出矩阵的计算公式如下：

公式有了，我们把复杂的空间几何问题转为数值计算，便于抽象理解和计算机的处理。该如何理解矩阵背后的几何意义呢？

2矩阵的几何意义

如上是两个二元一次方式组，不难推算，X = 1，Y=2是方程组的解。该方式式对应的矩阵形式如下：

对应的行优先对应的几何意义如下，红线代表方程式一，蓝线代表方式式二，两条直线相交于(1,2)。

Row Picture

我们在看看列有限的几何意义，此时矩阵分解为：

我们来看看其对应的向量意义：

如上图，分别是向量[1,2]和[-1,1]，我们已经知道x和y的值分别为1，2。如上图，我们把向量[-1,1]延长2倍，也就是[-2,2]，然后将该向量平移到[1,2]点，也就是向量1的终点，如下图，就是向量加的计算过程，[1,2] + [-1,1] *2 = [-1,4]，几何意义就是在该向量偏移量的累加。

Col Picture

矩阵之所以能够解决坐标转换问题，正是因为其Col Picture所体现的向量意义。现在，我们再体会一下之前的矩阵，是否有一点亲切。

3优化

如上是矩阵公式推算和几何意义的解释。看上去是几何问题，实际上是函数问题，这正是矩阵的价值所在。但函数问题也有一个缺点，特别是矩阵，计算量太大，占用内存也不低。大家在做数学题的时候应该都有过类似感觉，一个代数题好复杂，计算了半天，还容易犯错，好不容易才得出答案。这时老师用几何的思路来求解，一目了然，如穿越虫洞般不费吹灰之力。

回到这个问题，我们把坐标转换抽象成矩阵问题，对应的几何意义就是该点的切面和法线。

假设是一个圆，如下，圆心到该点就是其切面法线，这个向量很容易得出，通过点乘可以很容易的得到法线对应该点的垂线。

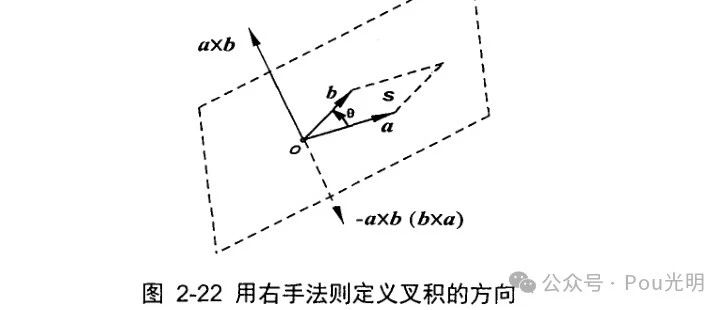
这时，把这个圆看成一个球，两条黑线的叉乘就可以得出另一个垂线，这就是该点对应的NEU坐标的三个轴，是不是也很容易理解，而且只需要三个步骤，计算量很小：

• 减法求出Up向量
• 点乘求出East向量
• 叉乘求出North向量

这正是Cesium中提供的思路，对应Transforms.eastNorthUpToFixedFrame方法，我就不当搬运工了，Over